在热力学的微观研究方面,玻尔兹曼(Boltzmann)论证了熵S与微观状态数的对数lnΩ之间的正比关系,普朗克将其总结为著名的玻尔兹曼熵公式S=klnΩ,把宏观量S与微观状态数Ω联系起来,在宏观与微观之间架起了一座桥梁,受熵概念的微观表述启发,程雪涛等人于2010年给出了单原子理想气体系统中火积的微观表达式,证明了当给出系统的粒子数、粒子质量和体积时,火积是微观状态数Ω的单值函数。而在工业与生活中,双原子气体的使用更为普遍,基于此,本文利用配分函数的近似计算,推导出了常温下双原子分子理想气体系统火积的微观表达式。如下图所示为双原子分子理想气体示意图。
与单原子气体分子仅考率电子配分函数、核配分函数、平动配分函数不同,双原子气体分子还需考虑转动配分函数与振动配分函数,且相应的配分函数与温度密切相关。如下图所示为分析框图。
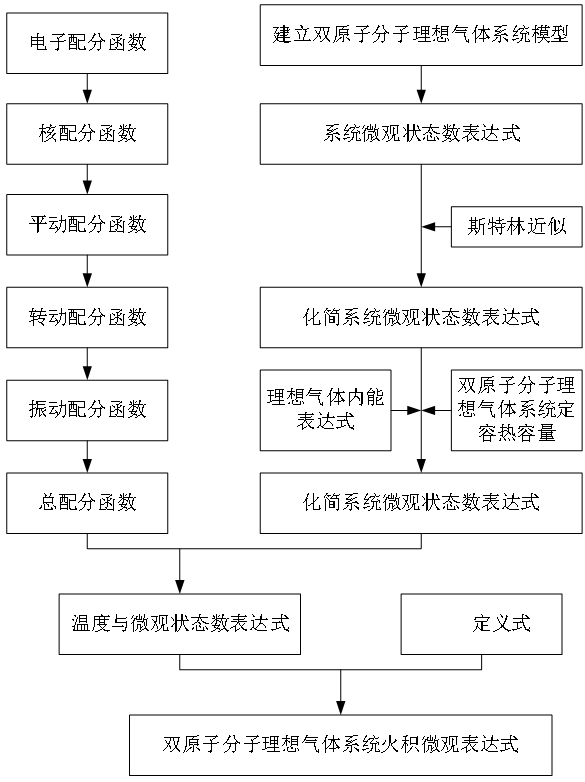
结果表明,对于一个系统内粒子数与体积不变的双原子分子理想气体系统,火积的微观表达式中微观状态数Ω的指数与单原子分子理想气体系统微观表达式中火积的指数不同,但火积仍是Ω的单值函数,其微观状态数越多,即意味着系统温度越高,因而系统的火积越大。


